PageRank
October 4, 2014 2 Comments
Suppose we compute PageRank with a β of 0.7, and we introduce the additional constraint that the sum of the PageRanks of the three pages must be 3, to handle the problem that otherwise any multiple of a solution will also be a solution. Compute the PageRanks a, b, and c of the three pages A, B, and C, respectively.
My R code is this.
M = matrix(c(0,1/2,1/2,0,0,1,0,0,1),ncol=3)
e = matrix(c(1,1,1),ncol=1)
v1 = matrix(c(1,1,1),ncol=1)
v1 = v1 / 3
for( i in 1:5){
v1 = ((0.7 * M ) %*% v1 ) + (((1 - 0.7 ) * e ) /3 )
}
v1 = v1 * 3
[,1]
[1,] 0.300
[2,] 0.405
[3,] 2.295
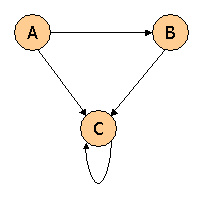
Hi,there. The node C is a dead end, so additional links to A and B should be added, therefor matrix M should be M = matrix(c(0,1/2,1/2,0,0,1,1/3,1/3,1/3),ncol=3). Besides, ‘e’ should be a n*n matrix, what do you think?
I remember the code generated values that were accepted by Coursera but I will check this.