Flow Matching and Diffusion Models

July 28, 2025 Leave a comment

I transcribe MIT 6.S184: Flow Matching and Diffusion Models – Lecture – Generative AI with SDEs. I try to do this using Tikz diagrams too.

tl:dr

  1. Ordinary Differential Equations have to be studied separately.
  2. Stochastic Differential Equations is a separate subject.
  3. I believe that I need to solve the exercises by coding to understand everything reasonably well.

Lecture 1

Conditional generation means sampling the conditional data distribution.

{ P_{data} (\bullet \mid y )}

Generative models generate samples from data distribution.

Initial Distribution : {P_{init} }

Default is {P_{init} \sim \mathcal{N}(0,{I}_d) }

Flow Model

Trajectory { X : \overbrace{[0,1]}^\text{Time component} \rightarrow \mathbb{R}^D} , t \rightarrow X_t So for each time component, t , we get a Vector out.

Vector Field. { u : \mathbb{R}^D x [0,1] \rightarrow \mathbb{R}^D} (There is a space component and Time component )

Flow

{ \psi \bullet \mathbb{R}^D x [0,1] \rightarrow \mathbb{R}^D}

{ (X_0, t) \rightarrow {\psi}_t(X_0)} means for every initial condition I want this to be a solution to my ODE.

{ {\psi}_0(X_0) = X_0 } which is the initial condition

.The time derivative of { \frac{d}{dt} {\psi}_t(X_0) } is { u_t ( {\psi}_t(X_0) }

Neural Network. { {{\psi}_t}^{\theta} \mathbb{R}^D x [0,1] \rightarrow \mathbb{R}^D}

Random Initialization { X_0 \rightarrow P_{init}}

Ordinary Differential Equation \frac{d}{dt} X_t = \psi_t^{\theta} X_t ( Time Derivative)

Goal Simulate to get { X_1 = P_{data}} 

{ \fbox{ TRAJECTORY } \rightarrow \fbox{ ODE } \overbrace{\leftarrow}^\text{defined by} \fbox{ VECTOR FIELD } }  
This means that Flow is a collection of Trajectories that conform to the ODE

Diffusion Model

Stochastic Process

{ X_t, 0 \leq t \leq 1} . { X_t } is a random variable

{ X : [0,1] \rightarrow \mathbb{R}^D , t \rightarrow X_t}

Vector Field. { u : \mathbb{R}^D x [0,1] \rightarrow \mathbb{R}^D} + Differential Coefficient

Stochastic Differential Equation

{X_0 = x_0 \left(\text {Initial} \\ \text {Condition} \right)}

The following means that the change of X_t in time is given by the change of direction of the Vector field {u_t X_t {dt}}

{{d}{X_t} = \underbrace{u_t X_t {dt}}_\text{ODE} + \underbrace{\sigma_t {d}{W_t}}_\text{Stochastic Noise} }

{{W_t} {\text{ is known as Brownian Motion}}}

Brownian Motion

Stochastic Process {W = {W_t}{(t=0)}} and in this case the time can be infinite. We don’t have to stop at {t = 1}

  1. {{W_0} = 0 }
  2. It has Gaussian increments. What does it mean ?

{{W_t} - {W_s} \thicksim \mathcal{N}(0,\,(t - s){I}_d) }

These are two arbitrary time points and t is before s, { 0 \leq t \leq s } and Variance of the Gaussian Distribution varies linearly with time.

3. Independent increments. This means that {{W_1} - {W_0} \ldots {W_n} - {W_{n-1}} }

So at this stage, in order to understand the following, I need a book or another course in ODE’s

\frac{d}{dt} X_t = u_t (X_t) \Leftrightarrow X_{t+h} = X_t + h u_t (X_t) + h (R_t(h)) \left( \displaystyle\lim_{h \to 0} \underbrace{R_t(h)}_\text{Error Term} = 0 \right)

This means the trajectory with ODE { u_t (X_t)} is equivalent to the timestep { X_t} plus h times the direction of the vector field { u_t {X_t}} plus a remainder term that can be ignored.

How are derivatives defined ?

This is the basic definition that I have to understand by learning Calculus.

Derivative of a trajectory \frac{d}{dt} X_t = u_t (X_t)

\frac{d}{dt} X_t = u_t (X_t) \Leftrightarrow \left( \displaystyle\lim_{h \to 0} \frac{X_{t+h} - X_t}{h} = u_t (X_t) \right)

\Leftrightarrow \left( \frac{(X_{t+h} - X_t)}{h} = u_t (X_t) + R_t(h) \right)

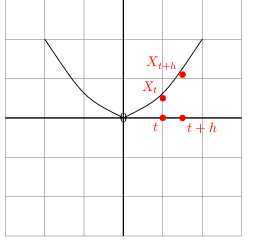
And by applying linear algebra we get the ODE shown above( this section ).

Ordinary Differential Equation to Stochastic Differential Equation

{d}X_t = u_t (X_t){dt} + \sigma {d} W_t

\Leftrightarrow X_{t+h} = X_t + h u_t (X_t) + \sigma_t \underbrace{(W_{t + h} - W_t)}_\text{Brownian Motion} + h R_t(h) \left( \displaystyle\lim_{h \to 0} \mathbb(E)[\sqrt {\lVert {R_t(h)} \rVert_2^2}] =0 \right)

This is the recap. We found a term that doesn’t depend on the derivatives that can be specified with an error term. \sigma_t is the diffusion coefficient used to scale the Brownian Motion. If \sigma_t is zero, it is equivalent to the original ODE.

Why do we need Brownian Motion ?

I didn’t really follow this. But the answer given was this. The Brownian Motion is equivalent to the Gaussian Distribution as far its universal value is concerned

Lecture 2

Reminder of what was covered in Lecture 1

\fbox{\begin{minipage}[t][.5cm]{0,4\textwidth} {\textbf{Flow Model}} \end{minipage}} \qquad {P_{init}} {\textbf{(Gaussian)}} \qquad {d}X_t = \overbrace{{{u_t}^{\theta} (X_t) {dt} }^\text{{\textbf{ODE}}}}

\fbox{\begin{minipage}[t][.8cm]{0,7\textwidth} \textbf{Diffusion Model} \end{minipage}} \qquad {P_{init}} {\textbf{(Gaussian)}} \qquad {d}X_t = \overbrace{ {u_t}^{\theta} (X_t){dt} + \underbrace{{\sigma}_t {d} W_t}_\text{{\textbf{Diffusion Co-efficient}}} }^\text{{\textbf{SDE}}}

Deriving a Training Target

Typically, we train the model by minimizing a mean-squared error

L_{\theta} = {\lVert {{u_t}^{\theta}(x) - {u_t}^{\mathrm{target}}(x)} \rVert_2^2}

In regression or classification, the training target is the label. Here we have no label. We have to derive a training target.

The professor states that you don’t have to understand all the derivations. I anticipate some mathematics I haven’t studied earlier.

We have to make sure we understand the formulas for these.

\begin{minipage}[t][.6cm]{0.9\textwidth} {\textbf{Conditional \\ Probability Path}} \end{minipage} \qquad \begin{minipage}[t][.6cm]{0.9\textwidth} {\textbf{Conditional \\ Vector field}} \end{minipage} \qquad \begin{minipage}[t][.6cm]{0.9\textwidth} {\textbf{Conditional \\ Score Function}} \end{minipage}

\begin{minipage}[t][.6cm]{0.9\textwidth} {\textbf{Marginal \\ Probability Path}} \end{minipage} \qquad \begin{minipage}[t][.6cm]{0.9\textwidth} {\textbf{Marginal \\ Vector field}} \end{minipage} \qquad \begin{minipage}[t][.6cm]{0.9\textwidth} {\textbf{Marginal \\ Score Function}} \end{minipage}

The key terminology to remember are the following.

\fbox{\begin{minipage}[t]{1,7\textwidth} \textbf{Conditional = Per Single data point \\ Marginal = Across distribution of data points } \end{minipage}}

Conditional and Marginal Probability Path

\textbf{ Dirac distribution : } z \in \underbrace{\mathbb{R}^d}_\text{Data we want to generate}, {\delta^z}

X \sim {\delta^z}, X = z, z \text{is the data point set}

This dirac distribution is not what I understand as of now. But it seems to return the same \textbf{z}

\textbf{ Conditional Probability Path : } \underbrace{P_t( \bullet \mid z)}_\text{Data we want to generate}, {\delta^z}

\textbf{ 1) } {P_t( \bullet \mid z)} \text{is a distribution over} {\mathbb{R}^d}

\textbf{ 2) } {P_0( \bullet \mid z) = P_{init} } \text{and} {P_1( \bullet \mid z) = {\delta^z}}

Example : Gaussian Probability Path

{P_0( \bullet \mid z) = \mathcal{N}({\alpha_t} z,{\beta_t}^2{I}_d) } }
{\alpha_t} \text{ and } {\beta_t} \text{ are termed noise schedulers }

{\beta_{\underbrace{1}_\text{Time 1}} =0} \\ {\beta_{\underbrace{0}_\text{Time 0}} =1} \\ {\alpha_{\underbrace{1}_\text{Time 1}} =1} \\ {\alpha_{\underbrace{0}_\text{Time 0}} =0}

The diagram is small. But the idea is that when Time is 0, mean is 0 and variance is 1 which is {P_{init} \sim \mathcal{N}(0,{I}_d) } and when Time is 1, mean is \textbf{z} and variance is 0.

The distributions with variance 1 is dirac, {\delta^z}

Example : Marginal Probability Path {P_t}

Well. This is not clear at this stage. But we take one data point(sampling) from {z \sim {P_{data} }} and marginal probability path means that we forget it. {\textbf{X} \sim {P( \bullet \mid z) }} \Rightarrow {\textbf{X} \sim P_t} . As far as I understand the data distribution and conditional distribution leads to the marginal path.

\textbf{Formula for the density is 1) } {\underbrace{{P_t( X )}}_\text{Likelihood at a point X}} {\int {(P_t \mid z)}} {P_{data} ( z ) } dz

The density formula is not clear at this stage.

\textbf{ 2) } {P_0 = P_{init}}, {P_1 = P_{data}}
All of this seems to describe that we move from noise to our distribution of the data we are dealing with.

Conditional and Marginal Vector Field

Conditional Vector field {{u_t}^{target} (X \mid Z)} \\ {0 \leq t \leq 1 } \\ {X,Z \in \mathbb{R}^d}

We want to condition such that starting from initial point

{\mathrm{P_0 = P_{Init}}} \textbf{ if we follow the vector field } {\frac{d}{dt} {X_t}} ={u_t}^{target}(X_t \mid z )

then the distribution of t at every time point is given by this probablity path \mathrm{ \Rightarrow {X_t \sim (\bullet \mid z)}}, \mathrm{0 \leq t \leq 1 }

We simulate the ODE like this.

Example : Conditional Gaussian Vector field

\dot{\alpha_t} is the time deritive and is from Physics

{u_t}^{target} (X \mid Z) = \left( \dot{\alpha_t} - {\frac{\dot{\beta_t}} {\beta_t}} \alpha_t \right) Z + {\frac{\dot{\beta_t}} {\beta_t}} X

Marginalization trick

The marginal vector field is {u_t}^{target} (X) = {\int {{u_t}^{target} (X \mid Z)}} \left( {\frac{{P_t (X \mid Z)} {P_{data} ( Z )}} {P_t (X) } } dz \right)

Not very clear at this point but the following is the application of the bayes rule to look at the posterior distribution. What could have been the data point from the point set Z that gave rise to X ?

\left( {\frac{{P_t (X \mid Z)} {P_{data} ( Z )}} {P_t (X) } } dz \right)

{\mathrm{P_0 = P_{Init}}} \textbf{ if we follow the vector field } {\frac{d}{dt} {X_t}} ={u_t}^{target}(X_t \mid z )

then the distribution of t at every time point is given by this marginal path \mathrm{ \Rightarrow {X_t \sim P_t}}, \mathrm{0 \leq t \leq 1 }

Conditional and marginal Score function

Conditional Score

\underbrace{ {\nabla {\log P_t( X \mid Z )}}}_\text{Gradient of log likelihood}

Marginal Score

\underbrace{ {\nabla {\log P_t( X )}}}_\text{Gradient of log likelihood}

Derivation

{\nabla {\log P_t( X )}} = \underbrace{ \nabla \left( {\frac{P_t( X )}{P_t( X )} } \right) } _\text{How is chain rule applied here ? }

Substituting the forumula show previously we get this after moving the gradient inside the integral.

= \nabla {\frac {{\int { {P_t( X \mid Z )} {P_{data}( Z )}}}} {{P_t (X)} }} dz = {\frac {{\int {\nabla {P_t( X \mid Z )} {P_{data}( Z )}}}} {{P_t (X)} }} dz

Using the result {\frac {d}{dx} {\log x}} = {\frac {1} {x} }

= {\int {\nabla {\log P_t( X )}} {\frac {{P_t( X \mid Z )} {P_{data}( Z )}} {{P_t (X)} }}} dz

What is the score of the Conditional Gaussian Vector Field ?

This derivation is out of range for me at the moment but the instructor mentioned this.

{u_t}^{target} (X \mid Z) = \left( \dot{\alpha_t} - {\frac{\dot{\beta_t}} {\beta_t}} \alpha_t \right) Z + {\frac{\dot{\beta_t}} {\beta_t}} X

\nabla {\log {P_t( X \mid Z )}} = X - {\frac{\alpha_t( Z )} {\beta_t^2} }

Theorem : SDE extension trick

\text{ Let } {u_t}^{target} (X) \text{ be as before } Then for any diffusion co-efficient {\alpha_t} \geq 0

{X_0 \sim {P_{init}}} , d{X_t} = \left[ {{u_t}^{target} (X_t)} + {\frac {{\alpha_t}^2}{2}} \nabla {\log {P_t( X_t )}} \right] dt + {\alpha_t} d{W_t} \Rightarrow {X_t \sim P_t}, {0 \leq t \leq 1}

{\sigma_t} is the noise injected.

Filed under Generative AI

Leave a comment